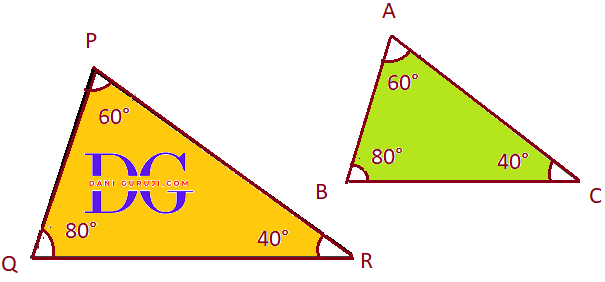
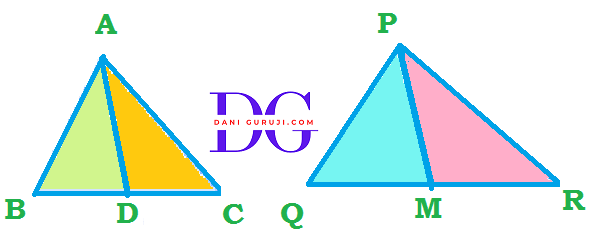
State which pairs of triangles In the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
Solution :
It is given that, In ∆ABC and ∆PQR,
$\angle $ A = $\angle $P = 60° , $\angle $B = $\angle $Q = 80° ,and $\angle $C = $\angle $R = 40° ,
Yes, the pairs of triangles are similar. The similarity criterion used is AAA (Angle-Angle-Angle) similarity.
( This criterion states that if the corresponding angles of two triangles are equal, then the triangles are similar.)
In this case, since all three corresponding angles of ΔABC and ΔPQR are equal, the triangles are similar.
Hence, ΔABC $\sim$ ΔPQR
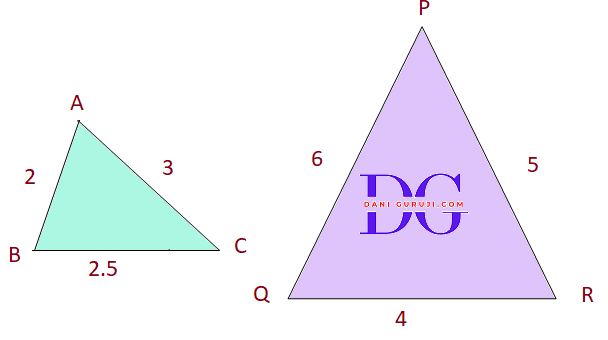
State which pairs of triangles In the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
Solution :
It is given that, In ∆ABC and ∆QRP,
$${AB \over QR} = {2 \over 4} = {1 \over2}$$
$${AC \over PQ} = {3 \over 6} = {1 \over2}$$
$${BC \over PR} = {2.5 \over 5} = {1 \over2}$$
$${AB \over QR} = {AC \over PQ} = {BC \over PR}$$
Yes, the pairs of triangles are similar. The similarity criterion used is SSS (Side-Side-Side) Similarity.
( This criterion states that if the corresponding sides of two triangles are proportional, then the triangles are similar.)
Since all the corresponding sides are in the same ratio (1/2), the triangles are similar.
Hence, ΔABC $\sim$ ΔQRP
State which pairs of triangles In the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
Solution :
It is given that, In ∆MPL and ∆EDF,
$${MP \over DE} = {2 \over 4} = {0.5}$$
$${LP \over DF} = {3 \over 6} = {0.5}$$
$${LM \over EF} = {2.7 \over 5} = 0.54$$
$${MP \over DE} = {LP \over DF} \ne {LM \over EF} $$
∆MPL and ∆EDF are not similar triangles because one pair of sides are not proportional to each other. Here, the ratio of ${LM \over EF}$ (0.54) is not equal to the ratios of the other two pairs of sides
$ ∆MPL \nsim ∆EDF $
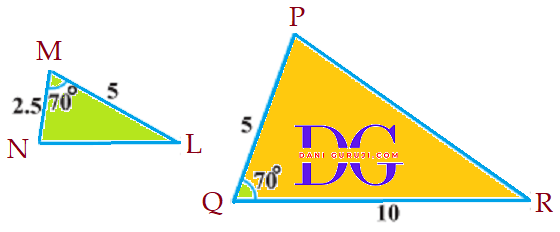
State which pairs of triangles In the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
Solution :
It is given that, In ∆MNL and ∆QPR,
$$\angle M = \angle Q = 70° $$
$${MN \over PQ} = {2.5 \over 5} = {1 \over2}$$
$${ML \over QR} = {5 \over 10} = {1 \over2}$$
$${ML \over QR} = {MN \over PQ} $$
Yes, the pairs of triangles are similar. The similarity criterion used is SAS (Side-Angle-Side) Similarity.
( This criterion states that if the One angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, the triangles are similar.)
$ ∆MPL \sim ∆EDF $
State which pairs of triangles In the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
Solution :
It is given that, In ∆ACB and ∆FDE,
$$\angle A = \angle F = 80° $$
$${AB \over FD} = {2.5 \over 5} = {1 \over2}$$
$${AC \over FE} = {AC \over 6} $$
$${AB \over FD} \ne {AC \over FE} $$
Given triangles are not similar because the corresponding angle is not contained by two corresponding sides.
Hence, ΔABC $\nsim$ ∆FDE
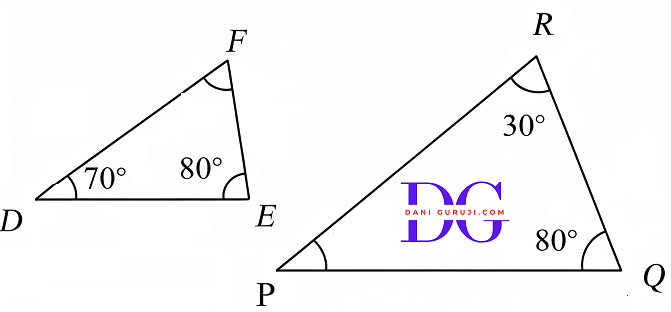
State which pairs of triangles In the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
Solution :
In triangle DEF, we have ,
$$\angle D + \angle E + \angle F = 180° $$
( By angle sum property of triangle )
$$ 70° + 80° + \angle F = 180° $$
$$\angle F = 30°$$
In triangle PQR, we have ,
$$\angle P + \angle Q + \angle R = 180° $$
( By angle sum property of triangle )
$$ \angle P + 80° + 30° = 180° $$
$$\angle P = 70°$$
In ∆DEF and ∆PQR
$$\angle E = \angle Q = 80°$$
$$\angle F = \angle R = 30° $$
$$\angle D = \angle P = 70°$$
All the corresponding angles of the triangles are equal.
Hence, By AAA criterion ΔDEF $\sim$ ΔPQR
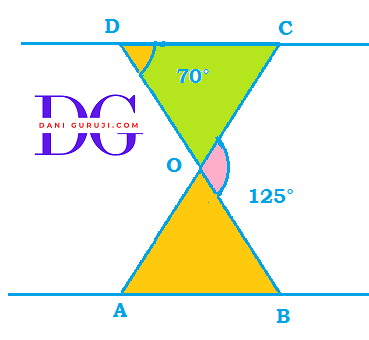
In the following figure. ∆OBA ~ ∆ODC, $\angle$ BOC = 125° and $\angle$CDO = 70°. Find $\angle$DOC, $\angle$DCO and $\angle$OAB.
Solution :
It is given that
$$ ∆OBA \sim ∆ODC $$
In ∆OBA and ∆ODC, we have
$$\angle OAB = \angle DCO $$
DOB is a straight line. So, $\angle$DOC and $\angle$BOC forms a linear pair
$$ \angle BOC + \angle DOC = 180° $$
$$ 125° + \angle DOC = 180° $$
$$ \angle DOC = 180°- 125° $$
$$ \angle DOC = 55° $$
Now ,In ∆ODC
$$ \angle DCO = (180°- (70° + 55°)) $$
$$ \angle DCO = 55° $$
$\angle$ OAB = $\angle$ DCO = 55° ( Alternate angles)
∴ $\angle$ DCO = 55° , $\angle$OAB = 55° and $\angle$DOC = 55°
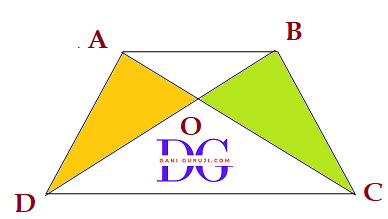
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $ {OA \over OC} = {OB \over OD} $
Solution :
It is given that,
the trapezium ABCD with AB || DC. The diagonals AC and BD intersect at point O
In ∆AOB and ∆COD, , we have
Since AB || DC and AC is a transversal, the alternate interior angles are equal.
$$ \angle OAB = \angle OCD $$
( Alternate interior angles )
Since AB || DC and BD is a transversal, the alternate interior angles are equal.
$$ \angle OBA = \angle ODC $$
( Alternate interior angles )
$$\angle AOB = \angle COD $$
(Vertically opposite angles)
by the AAA (Angle-Angle-Angle) similarity criterion $$ ⇒ ∆AOB \sim ∆COD $$
( When two triangles are similar, the ratio of their corresponding sides is equal. Therefore, from the similarity of ∆AOB and ∆COD , we can write:)
Hence, $ {OA \over OC} = {OB \over OD} $
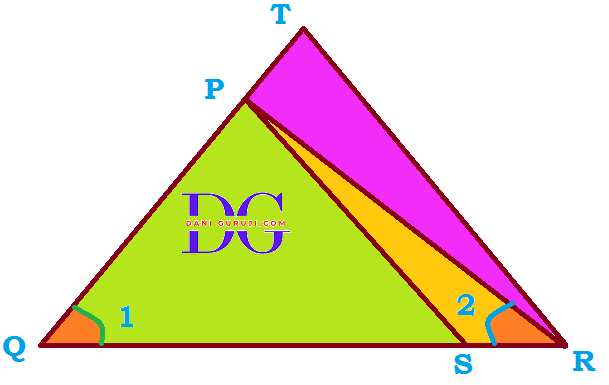
In the following figure. $ {QR \over QS} = {QT \over PR} $ and $\angle$1 = $\angle$2. Show that ∆PQS ~ ∆TQR.
Solution :
It is given that,
In ∆PQR , $\angle$1 = $\angle$2
$$ ⇒ PR = PQ $$
( Since angles opposite to equal sides of a triangle are equal, then the sides opposite to these angles must also be equal.)
It is given that
$$ {QR \over QS} = {QT \over PR}$$
Since we know that PR = PQ, we can replace PR with PQ in the equation.
$$⇒ {QR \over QS} = {QT \over PQ}$$
In ∆PQS and ∆TQR
$$⇒ {QR \over QS} = {QT \over PQ}$$
$$ \angle PQS = \angle TQR $$
(Since we have shown that two pairs of corresponding sides are proportional and their included angles are equal ($ \angle PQS = \angle TQR $) . We can conclude that the triangles are similar by the SAS (Side-Angle-Side) Similarity Criterion.)
Therefore, $$ ∆PQS \sim ∆TQR $$
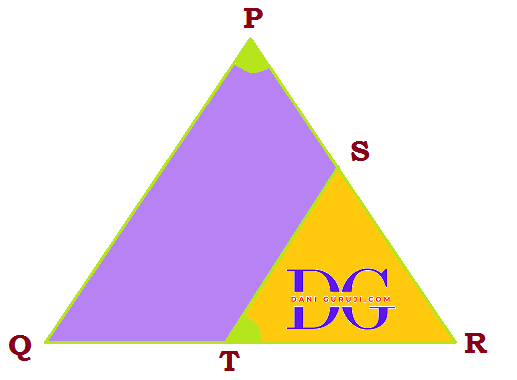
S and T are points on sides PR and QR of ∆PQR such that $\angle$ P = $\angle$ RTS. Show that ∆RPQ ~ ∆RTS.
Solution :
It is given that,
$\angle$ P = $\angle$ RTS
In ΔRPQ and ΔRTS, we have
$$ \angle RPQ = \angle RTS $$
( Given )
$$ \angle PRQ = \angle TRS $$
(Common angle )
Since we have found two pairs of corresponding angles that are equal, we can conclude that the triangles are similar.
Thus, by the AA similarity criterion, we can state that
$$ ∆RPQ \sim ∆RTS $$
In the given fIgure. ∆ABE $\cong $ ∆ACD. show that ∆ADE ~ ∆ABC
Solution :
It is given that
∆ABE $\cong $ ∆ACD
Since the triangles are congruent, their corresponding parts are equal.
$$ AB = AC ............(i)$$
(corresponding sides by CPCT )
$$ AE = AD $$
$$ AD = AE ............(ii)$$
(corresponding sides by CPCT )
Now Consider ΔADE and ΔABC
Dividing Eq.(ii) by Eq.(i)
$$ { AD \over AB } = { AE \over AC}$$
(A pair of corresponding sides are in proportion )
$$ \angle DAE = \angle BAC $$
(Common angle )
Therefore, by the SAS similarity criterion, we have proven that,
$$ ∆ADE \sim ∆ABC $$
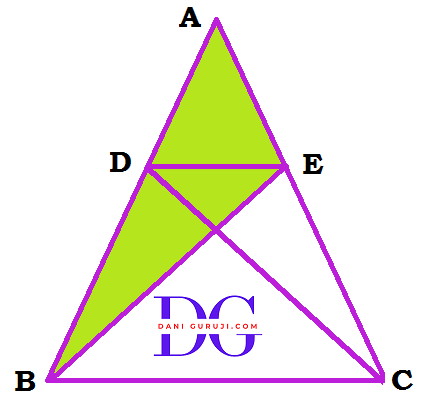
In following figure. attitudes AD and CE of ∆ABC Intersect each other at the point P. Show that:
(i) ∆AEP ~ ∆CDP
(ii) Δ ABD ~ Δ CBE
(iii) Δ AEP ~ Δ ADB
(iv)Δ PDC ~ Δ BEC
Solution :
(i) ∆AEP ~ ∆CDP
$$ \angle AEP = \angle CDP = 90° $$
(Both are Right angle Because CE⊥AB and AD⊥BC )
$$ \angle APE = \angle CPD $$
(Vertically Opposite angles )
$$ Δ AEP \sim Δ CDP $$
(Therefore by AA criterion of similarity )
Hence proved
(ii) Δ ABD ~ Δ CBE
$$ \angle ADB = \angle CEB = 90° $$
(Both are Right angle )
$$ \angle ABD = \angle CBE $$
(Common angle )
$$ Δ ABD \sim Δ CBE $$
(Therefore by AA criterion of similarity )
Hence proved
(iii) Δ AEP ~ Δ ADB
$$ \angle AEP = \angle ADB = 90° $$
(Both are Right angle )
$$ \angle PAE = \angle DAB $$
(Common angle )
$$ Δ AEP \sim Δ ADB $$
(Therefore by AA criterion of similarity )
Hence proved
(iv) Δ PDC ~ Δ BEC
$$ \angle PDC =\angle BEC= 90° $$
(Both are Right angle )
$$ \angle PCD = \angle BCE $$
(Common angle )
$$ Δ PDC \sim Δ BEC $$
(Therefore by AA criterion of similarity )
Hence proved
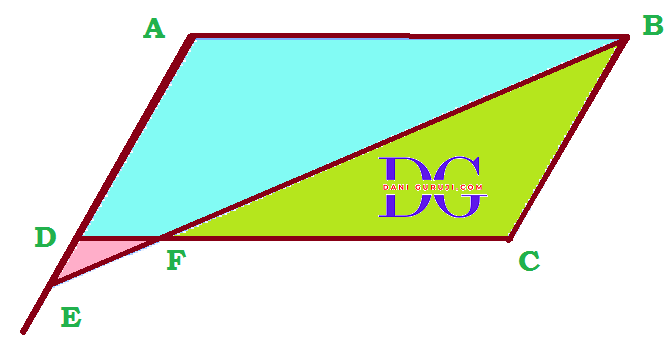
E is a point on the side AD produced of a parallelogram ABCD and BE Intersects CD at F. Show that ∆ABE ~ ∆CFB.
Solution :
In a parallelogram ABCD ,
Opposite angles of a parallelogram are equal
$$ \angle A = \angle C .........(i) $$
Also , Opposite Sides of a parallelogram are parallel
$$ AD || BC $$
AE is extension of AD so,
$$ AE || BC $$
And BE is traversal,
$$ \angle AEB = \angle CBF ............(ii)$$
(is a transversal alternate angle )
Now Consider Δ ABE and Δ CFB
$$ \angle A = \angle C $$
from eq. (i)
$$ \angle AEB = \angle CBF $$
from eq. (ii)
$$ ∆ABE \sim ∆CFB $$
(Therefore by AA criterion of similarity )
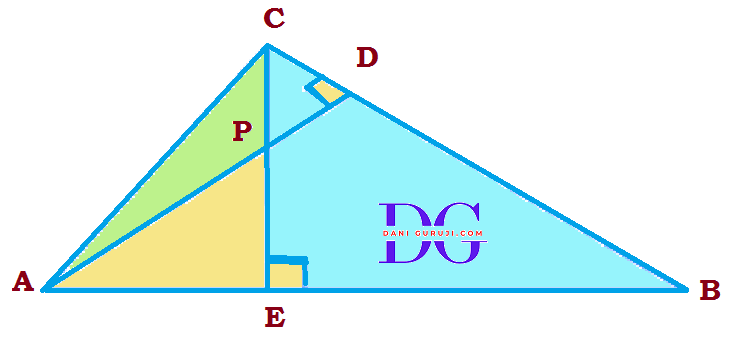
In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:
(i)$ ∆ABC \sim ∆AMP $
(ii)$$ {CA \over PA } = {BC \over MP } $$
Solution :
(i) ∆ABC ~ ∆AMP
In Δ ABC and Δ AMP
$$ \angle ABC = \angle AMP = 90° $$
(Both are Right angle )
$$ \angle BAC =\angle MAP $$
(Common angle )
$$ Δ ABC \sim Δ AMP $$
(Therefore by AA criterion of similarity )
Hence proved .
(ii)
Since we have already proven that $ Δ ABC \sim Δ AMP $, the ratio of their corresponding sides must be equal.
( As we know that the ratio of any two corresponding sides in two similar triangles is always the same,, we can write: )
$$ {CA \over PA } = {BC \over MP } $$
Hence proved
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively.
If ∆ABC ~ ∆EFG, show that
(i) $ {CD \over GH } = {AC \over FG } $
Solution :
(i) To Prove $ {CD \over GH } = {AC \over FG } $
Given,
$ ∆ABC \sim ∆EFG $
$$ ⇒ \angle A = \angle F , \angle B = \angle E , \angle ACB = \angle FGE $$
(When two triangles are similar, their corresponding sides are in proportion and their corresponding angles are equal. )
$$ ⇒ \angle ACB = \angle FGE $$
$$ ⇒ {{\angle ACB} \over 2 } = {{\angle FGE} \over 2 } $$
$$ ⇒ \angle ACD = \angle FGH $$
(Because CD and GH are bisectors of ∠C and ∠G respectively. )
now, In Δ ACD and Δ FGH
$$ ∵ \angle ACD = \angle FGH $$
(proved above )
$$ \angle A = \angle F $$
( $ ∆ABC \sim ∆EFG $ )
Therefore, By the AA (Angle-Angle) similarity criterion
$$ Δ ACD \sim Δ FGH $$
Since the triangles are similar, the ratio of their corresponding sides is equal:
$$ {CD \over GH } = {AC \over FG } $$
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively.
If ∆ABC ~ ∆EFG, show that
(ii) $ ∆ DCB \sim ∆ HGE $
Solution :
(ii) To Prove $ ∆ DCB \sim ∆ HGE $
Given,
$ ∆ABC \sim ∆EFG $
$$ ⇒ \angle A = \angle F , \angle B = \angle E , \angle ACB = \angle FGE $$
(When two triangles are similar, their corresponding sides are in proportion and their corresponding angles are equal. )
$$ ⇒ \angle ACB = \angle FGE $$
$$ ⇒ {{\angle ACB} \over 2 } = {{\angle FGE} \over 2 } $$
$$ ⇒ \angle BCD = \angle EGH $$
(Because CD and GH are bisectors of ∠C and ∠G respectively. )
now, In Δ BCD and Δ EGH
$$ ∵ \angle BCD = \angle EGH $$
(proved above )
$$ \angle B = \angle E $$
( $ ∆ABC \sim ∆EFG $ )
Therefore, By the AA (Angle-Angle) similarity criterion
$$ Δ BCD \sim Δ EGH $$
OR
$$ Δ DCB \sim Δ HGE $$
Hence proved
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively.
If ∆ABC ~ ∆EFG, show that
(iii) $ ∆ ∆DCA \sim ∆ HGF $
Solution :
(ii) To Prove $ ∆ ∆DCA \sim ∆ HGF $
Given,
$ ∆ABC \sim ∆EFG $
$$ ⇒ \angle A = \angle F , \angle B = \angle E , \angle ACB = \angle FGE $$
(When two triangles are similar, their corresponding sides are in proportion and their corresponding angles are equal. )
$$ ⇒ \angle ACB = \angle FGE $$
$$ ⇒ {{\angle ACB} \over 2 } = {{\angle FGE} \over 2 } $$
$$ ⇒ \angle ACD = \angle FGH $$
(Because CD and GH are bisectors of ∠C and ∠G respectively. )
now, In Δ ACD and Δ FGH
$$ ∵ \angle ACD = \angle FGH $$
(proved above )
$$ \angle A = \angle F $$
( $ ∆ABC \sim ∆EFG $ )
Therefore, By the AA (Angle-Angle) similarity criterion
$$ Δ ACD \sim Δ FGH $$
OR
$$ Δ DCA \sim Δ HGF $$
Hence proved
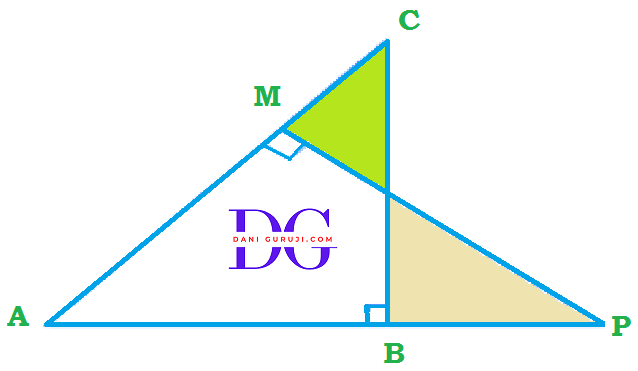
In the given figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that Δ ABD ∼ Δ ECF.
Solution :
To Prove $ Δ ABD \sim Δ ECF $
Here, Δ ABC is isosceles triangle with AB = AC
$$ ⇒ \angle B = \angle C $$
( Angles opposite to equal sides are also equal. )
In Δ ABD and Δ ECF, right-angled triangles
AD⊥BC, and EF⊥AC, which means,
$$ ∵ \angle ADB = \angle EFC = 90° $$
(Both are Right angle )
$$ ⇒ \angle ABD = \angle ECF $$
(Because $ \angle $ B = $ \angle $ C )
By the AA similarity criterion, we can conclude that :
$$ Δ ABD \sim Δ ECF $$
Hence proved
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of Δ PQR. Show that Δ ABC ~ Δ PQR.
Solution :
To Prove $ Δ ABC \sim Δ PQR $
Given :
In triangle Δ ABC and Δ PQR
$$ ⇒ {AB \over PQ} = {BC \over QR}= {AD \over PM} $$
AD is the median of △ABC, so D is the midpoint of BC
$$ ⇒ BD = CD = {{1 \over 2 }BC} $$
PM is the median of △PQR, so M is the midpoint of QR
$$ ⇒ QM = RM = {{1 \over 2 }QR} $$
Now In Δ ABD and Δ PQM ,
$$ {AB \over PQ} = {BC \over QR}= {AD \over PM} $$
$$ ⇒ {AB \over PQ} = {2BD \over 2QM}= {AD \over PM} $$
$$ ⇒ {AB \over PQ} = {BD \over QM}= {AD \over PM} $$
Since the ratios of all three corresponding sides of △ABD and △PQM are equal, the triangles are similar by the SSS (Side-Side-Side) similarity criterion.
Therefore, $$ Δ ABD \sim Δ PQM $$
$$ ∵ \angle B = \angle Q $$
(corresponding angles of similar triangles are equal )
Now In Δ ABC and Δ PQR ,
$$ ⇒ {AB \over PQ} = {BC \over QR} $$
(Given statement )
$$ ⇒ \angle ABC = \angle PQR $$
( From the similarity of the smaller triangles, we know that $ \angle$ B = $ \angle$ Q ,proved above )
Since two pairs of corresponding sides are proportional and the included angles are equal, by the SAS (Side-Angle-Side) similarity criterion.
$$ Δ ABC \sim Δ PQR $$
Hence proved
D is a point on the side BC of a triangle ABC such that $ \angle$ ADC = $ \angle$ BAC. Show that CA2 = CB.CD
Solution :
To Prove CA2 = CB.CD
Given : $\angle$ ADC = $\angle$ BAC
In Δ BAC and Δ ADC
$$ ⇒ \angle BAC = \angle ADC $$
Given in the statement
$$ \angle ACB = \angle DCA $$
Common angle
Therefore we can say that the triangles are similar by the AA (Angle-Angle) similarity criterion.
$$ Δ BAC \sim Δ ADC $$
$$ ⇒ {CA \over CB} = {CD \over CA} $$
(Because the triangles are similar, the ratio of their corresponding sides is equal. )
$$ ⇒ {CA^2} = {CD × CB} $$
Hence proved
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another Δ PQR. Show that Δ ABC ~ Δ PQR.
Solution :
To Prove $ Δ ABC \sim Δ PQR $
Given :
In triangle Δ ABC and Δ PQR
$$ ⇒ {AB \over PQ} = {AC \over PR}= {AD \over PM} $$
Now In Δ ABC and Δ PQR
Construction
Produce AD and PM to E and L such that AD = DE and PM = ML.
Now, join B to E,C to E,and Q to L and R to L.
AD and PM are medians of a triangle, We know that medians is the bisector of opposite side.
therefore BD = DC and QM = MR
AD = DE and PM = ML
(By construction )
Hence in quadrilateral ABEC
diagonals AE and BC bisecting each other at D,so ABEC is a parallelogram
Similarly, quadrilateral PQLR is also a parallelogram.
Therefore, AC = BE ,AB = EC and PR = QL,PQ = LR ...........(i)
(Opposite sides of a parallelogram are equal )
Now In Δ ABE and Δ PQL ,
$$ ⇒ {AB \over PQ} = {AC \over PR}= {AD \over PM} $$
(Given statement )
$$ ⇒ {AB \over PQ} = {BE \over QL}= {AD \over PM} $$
(From Eq. 1 )
$$ ⇒ {AB \over PQ} = {BE \over QL}= {2AD \over 2PM} $$
$$ ⇒ {AB \over PQ} = {BE \over QL}= {AE \over PL} $$
( 2AD= AE = AD + DE and 2PM = PL = PM + ML)
( where AD = DE and PM = ML by construction)
$$∴ Δ ABE \sim Δ PQL $$
(Therefore by SSS criterion of similarity )
$$ Hence, \angle BAE = \angle QPL ...........(ii)$$
(corresponding angles of similar triangles are equal )
Similarly we can prove that
In Δ AEC and Δ PLR ,
$$∴ Δ AEC \sim Δ PLR $$
$$ Hence, \angle CAE = \angle RPL ...........(iii)$$
(corresponding angles of similar triangles are equal )
Adding Eq. (ii) and (iii)
$$ ⇒ \angle BAE + \angle CAE = \angle QPL + \angle RPL $$
$$ ⇒ \angle BAC = \angle QPR ...........(iv)$$
Now In Δ ABC and Δ PQR ,
$$ ⇒ {AB \over PQ} = {AC \over PR} $$
(Given statement )
$$ ⇒ \angle BAC = \angle QPR $$
(From Eq. 4 )
(Therefore by SAS criterion of similarity )
$$ Δ ABC \sim Δ PQR $$
Hence proved
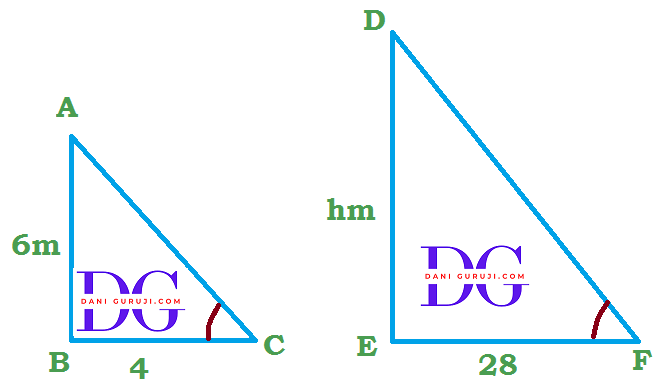
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution :
We can solve this problem by using the concept of similar triangles. At the same time of day, the sun's rays hit the ground at the same angle.
This means that a vertical pole and its shadow, and a vertical tower and its shadow, form two similar right-angled triangles.
Given : Height of pole AB = 6 meter and its shadow = BC = 4 m
Shadow of tower = EF = 28 meter.
To find : Height of tower DE = h meter.
In Δ ABC and Δ DEF,
$$ \angle B = \angle E = 90°$$
(Both are vertical to ground )
$$ \angle C = \angle F $$
(The angle of elevation of the sun will be same at a given time for both the triangles. )
$$ Δ ABC \sim Δ PQR $$
( If two angles of one triangle are respectively equal to the two angles of another triangle, then the two triangles are similar.This is referred to as the AA criterion.)
Hence, $$ {AB \over DE} = {BC \over EF} $$
( Because in case of two similar triangles, the ratio of their corresponding sides are equal)
$$ {6 \over h} = {4 \over 28} $$
$$ ⇒ h = {{6 × 28} \over 4} $$
$$ ⇒ h = 42 $$
Hence, the height of the tower = h = 42 metres.
If AD and PM are medians of triangles ∆ABC and ∆PQR respectively, where ∆ABC ~ ∆PQR. prove that $ {AB \over PQ} = {AD \over PM} $.
Solution :
To Prove : $ {AB \over PQ} = {AD \over PM} $
Given :
$$ Δ ABC \sim Δ PQR $$
∴ we have $$ {AB \over PQ} = {BC \over QR}= {AC \over PR} $$
In Δ ABC and Δ PQR ,
D is the mid-point of BC. $$ ⇒ BD = CD = {{1 \over 2 }BC} $$
M Is the mid-point of QR.$$ ⇒ QM = RM = {{1 \over 2 }QR} $$
∵ AD and PM are median of ΔABC and ΔPQR respectively
$$ ∴{AB \over PQ} = {BC \over QR} $$
$$ ⇒{AB \over PQ} = {2BD \over 2QM} $$
$$ ⇒{AB \over PQ} = {BD \over QM} .......(i) $$
$$ Since , Δ ABC \sim Δ PQR $$
$$ \angle B = \angle Q ......(ii)$$
(Corresponding angles of similar triangles are equal )
Now In Δ ABD and Δ PQM ,
$$ {AB \over PQ} = {BD \over QM} $$
(From Eq. i )
$$ \angle B = \angle Q $$
(From Eq. ii )
(Therefore by SAS criterion of similarity )
$$ Δ ABD \sim Δ PQM $$
$$ ⇒ {AB \over PQ} = {AD \over PM} $$
(corresponding sides are in same ratio )
Hence proved
Syllabus for class 10
Advanced courses and exam preparation.
Previous Year Paper
Advanced courses and exam preparation.
Mock Test
Explore programming, data science, and AI.